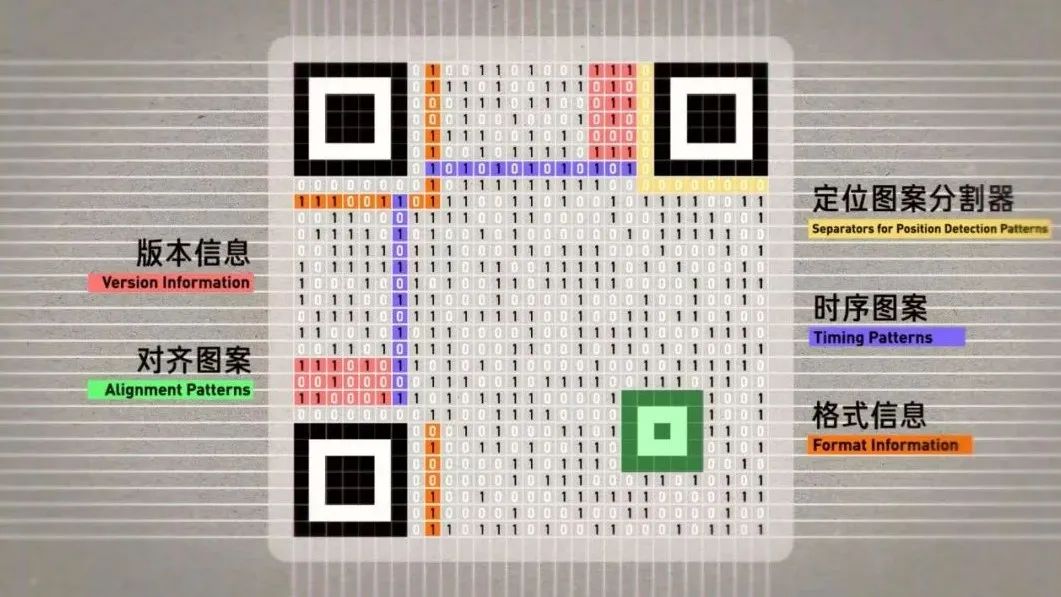
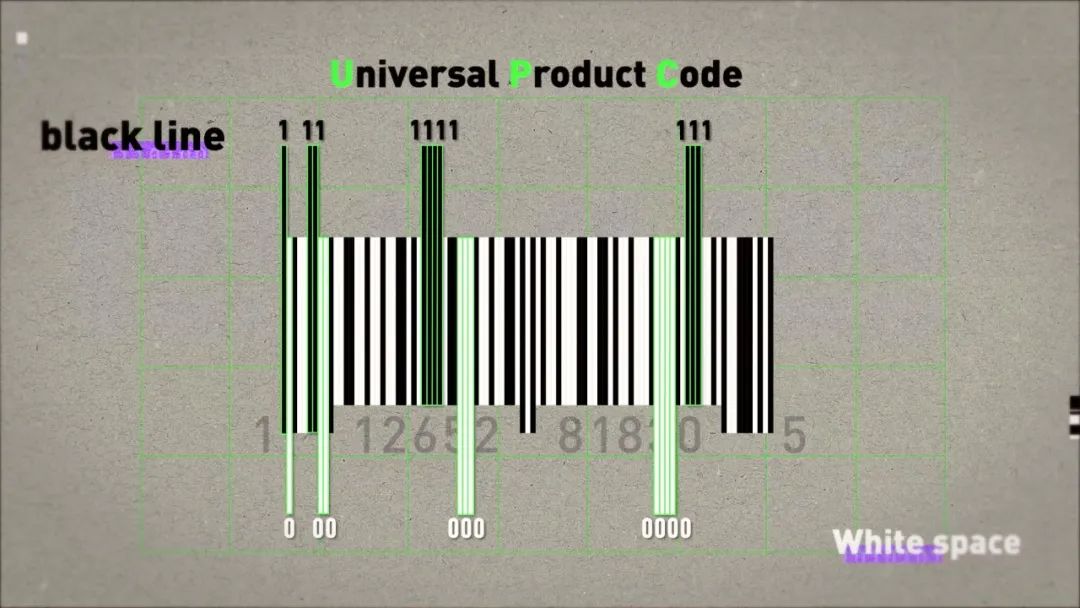
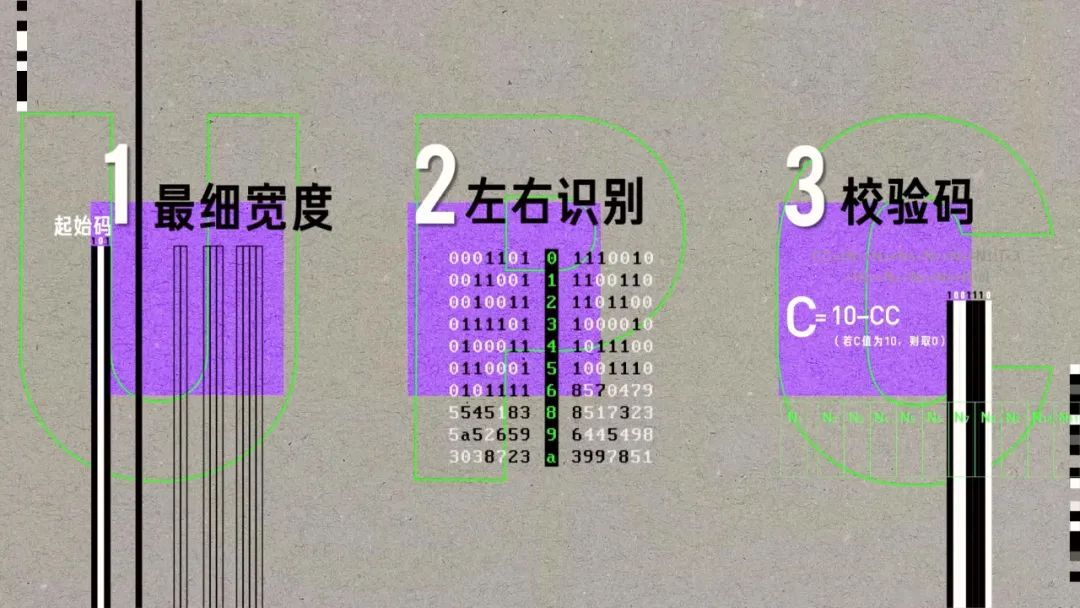
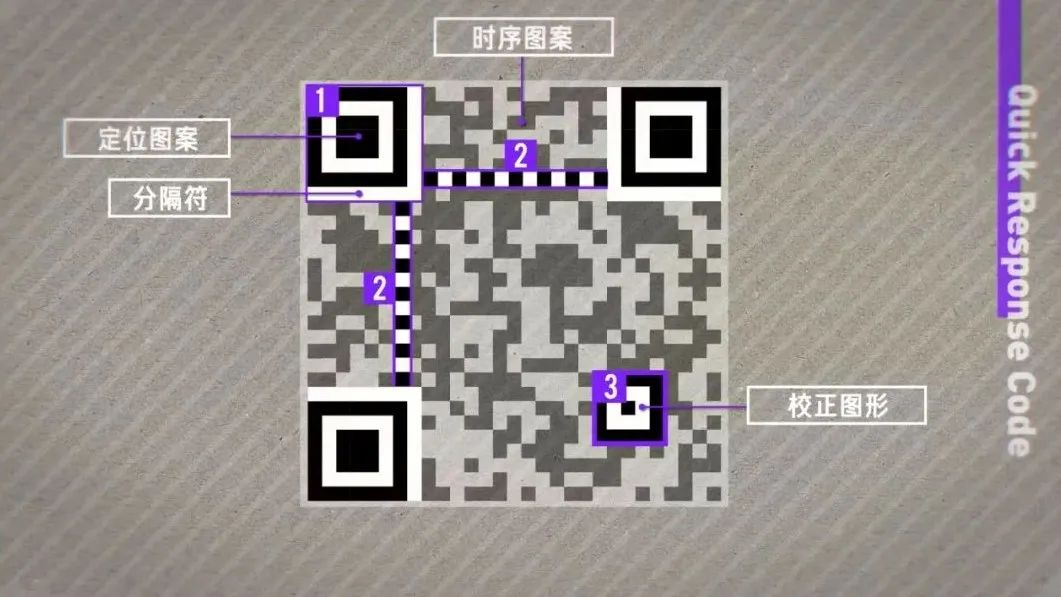
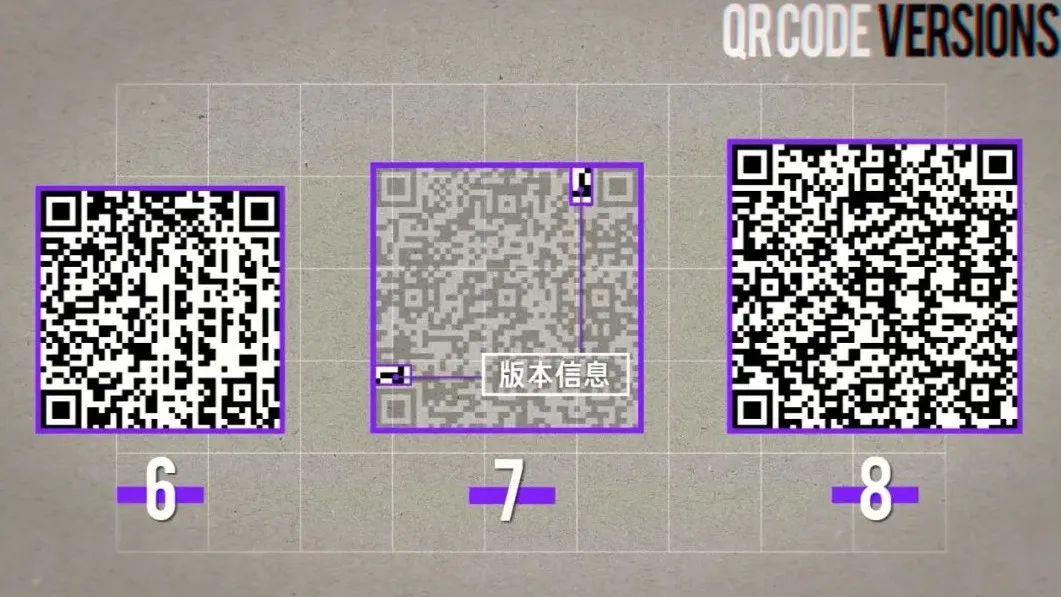
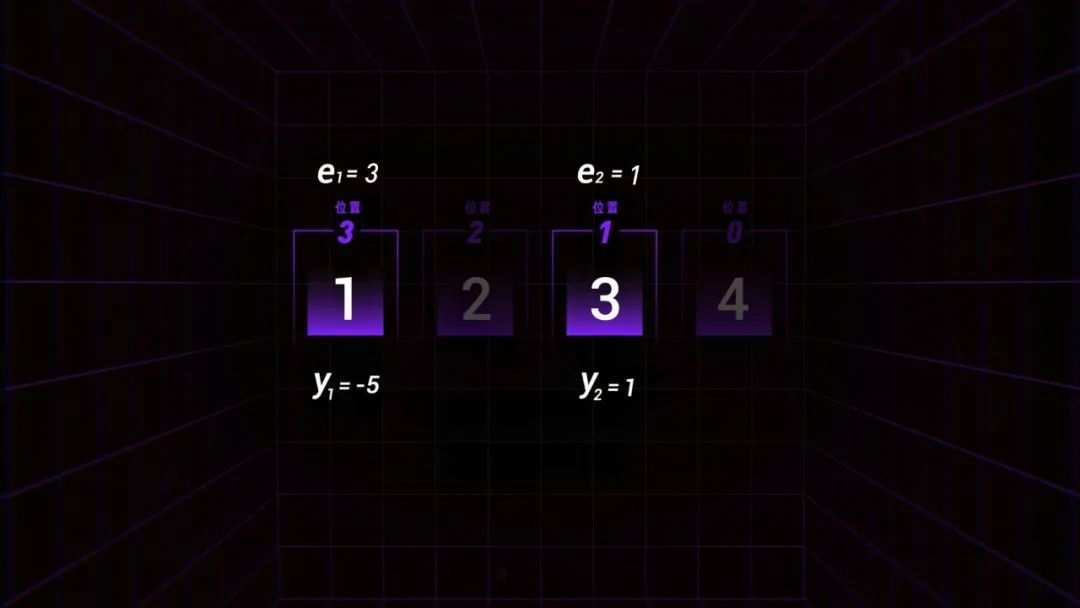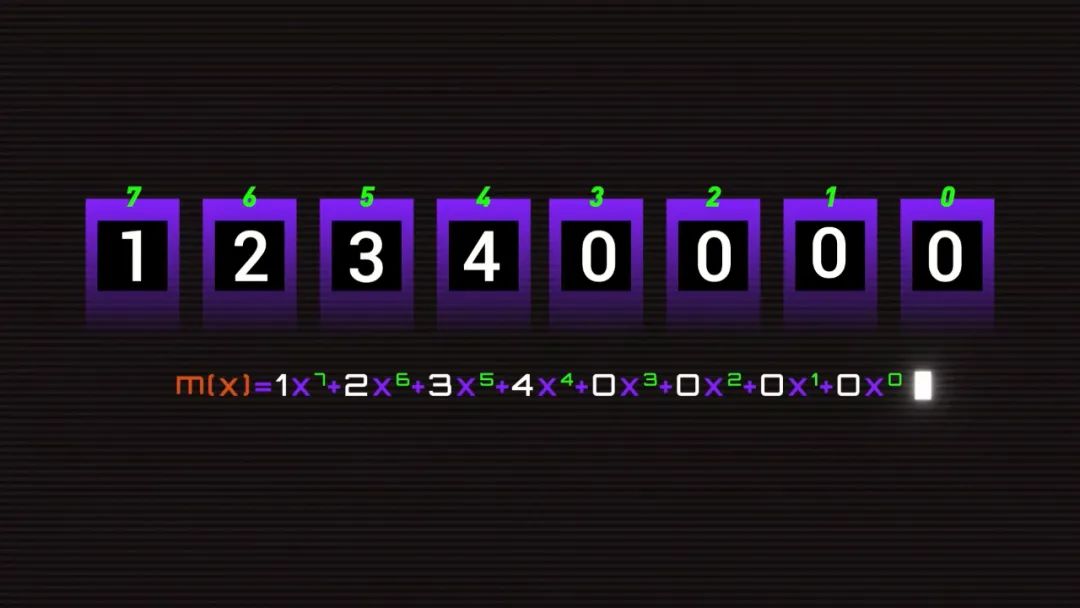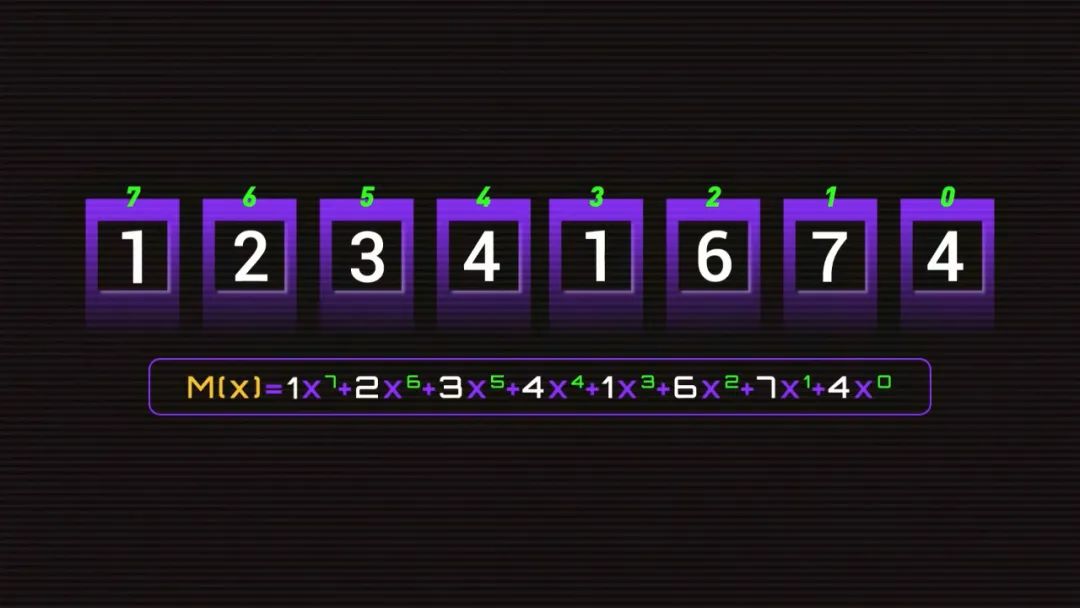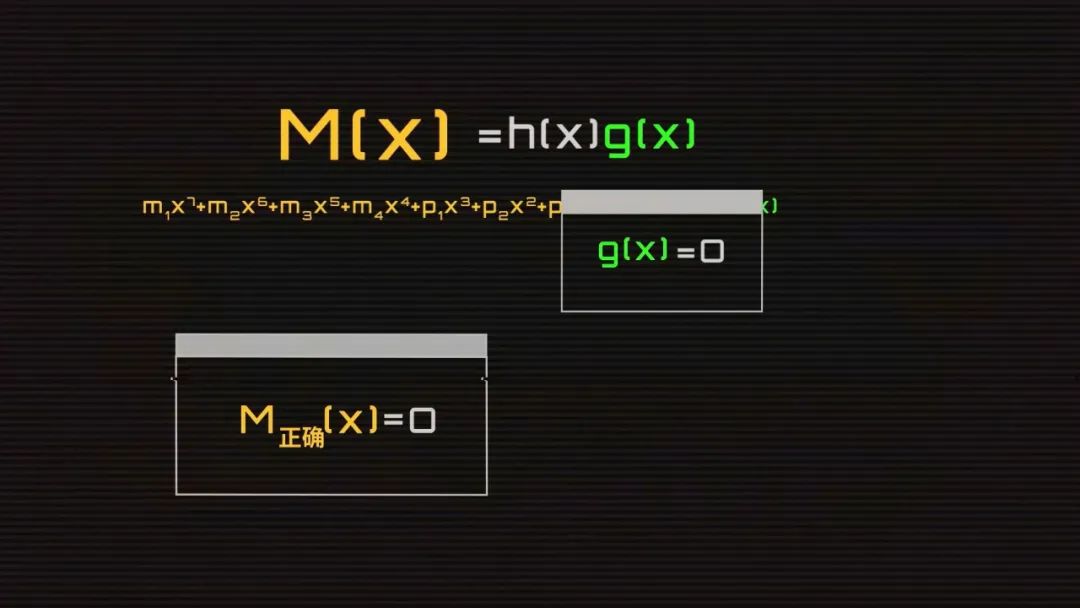加人、購物、填表、付錢，你可能掃過無數(shù)次二維碼，但卻從來沒有認真看過它。這個二維碼結(jié)構(gòu)看起來很簡單，左下、左上和右上有三個方塊用來定位。剩下的位置就是一堆黑色和白色小方塊組成一個 29×29 的大方塊，白色方塊表示 0，黑色方塊表示 1。由這些 0 和 1 構(gòu)成的二進制字符串就可以轉(zhuǎn)換成各種數(shù)字、字母和符號了。但你仔細看，就會發(fā)現(xiàn)沒這么簡單。條碼系統(tǒng)誕生之初，就是希望創(chuàng)造一套簡單清晰可被印刷能被機器識別的圖形編碼，讓機器輕松獲取商品編號。這樣你在超市買東西的時候，收銀員就不需要手動記錄，只需要掃一下就能知道多少錢了。這就是二維碼的前身——一維碼，今天我們都叫條形碼。以 UPC（Universal Product Code）碼為例，本質(zhì)上就是 30 條粗細不一的黑線。而黑色豎線和白色間隔的寬度，就是隱藏在條形碼里的二進制信息。豎線和間隔都有 4 種寬度。最細的豎線代表一個 1，之后是兩個 1，三個 1，最粗的豎線就是 4 個 1。對應的，4 種間隔寬度就是 0、00、000、0000。比如這里，就是 0110001，根據(jù)編碼表，代表 5。每 2 條豎線加 2 條間隔就能表示一個數(shù)字，這 48 條豎線和間隔就可以表示 12 位數(shù)字編號了。而左右最外側(cè)的雙排線則是所有條碼的固定開頭，代表 101，這么做的意義在于讓掃碼器知道這個條碼最細寬度，進而識別出這個寬度的 2、3、4 倍。這樣，無論條碼按照什么尺寸印刷，掃碼器都可以完成識別，需要的信息也只有一條線這么多，其他地方都污損了也沒關系。只要讓掃碼器區(qū)分左右就好了。我們把分隔符左側(cè)的編碼表里的 0 變成 1、1 變成 0 ，就得到了分隔符右側(cè)的編碼表。巧妙的地方在于，左側(cè)所有組合里 1 的個數(shù)都是奇數(shù) ，而右側(cè)都是偶數(shù)。這樣，掃碼器從左往右讀取數(shù)據(jù)時只要發(fā)現(xiàn)一組數(shù)據(jù)里的 1 是偶數(shù)，那么就可以確認掃反了。用逆碼表解讀數(shù)字，再重新組合，就能得到正確編號。最后，編號第 12 位數(shù)是根據(jù)前 11 位數(shù)計算出來的校驗碼，以防止篡改。這三重設計保證了條形碼可以適應各種復雜的現(xiàn)實情況，非常可靠。但條形碼上能承載的信息還是太少了，所以，以矩陣形式承載更多信息的二維碼出現(xiàn)了。在這些奇奇怪怪的二維碼中， QR 碼脫穎而出，出現(xiàn)在了你的微信支付寶和火車票上。QR 的全稱是 Quick Response，快速響應矩陣。最有代表性的就是這三個回字型方塊，這樣的排布方案可以讓你無論從哪個方向掃描二維碼都會自動校正為正確方向，只要右下角沒方塊就是對的，很簡單。但 QR 碼是怎么實現(xiàn)校驗、糾錯同時保證準確度的呢？我們找到了這份 126 頁的 QR 碼國際通用標準。今天的普通 QR 碼有 40 個版本，版本越大，尺寸越大。最小的版本 1 是一個 21×21 的正方形，版本號每加 1，正方形的邊長就多 4 格。最大的版本 40 就是一個這樣 177×177 的密恐正方形。以這個版本 3 的 QR 碼為例，大概由 5 個部分組成。1 是 3 個7×7 的回字形方塊和寬度為 1 的白色的分隔符。2 是這兩條黑白相間的定位圖案，告訴掃碼器橫豎的標準方向。3 是右下角的校正圖形，一個 5×5 的小方塊，尺寸越大，校正圖形越多。這樣，即使你用奇怪的角度掃描，算法依然可以根據(jù)這三組圖案提取輪廓，修正透視，獲得正面圖案。4 是由相同的兩組方塊組成的格式信息，每組 15 個，放置在定位方塊的旁邊。5 作為剩下的區(qū)域，會被分成 8 個一組的模塊，存儲數(shù)據(jù)和糾錯碼。而在大于等于版本 7 的 QR 碼里，還需要在這兩處記錄 18 位的版本信息，提高掃碼器的效率。1、2、3 的設計只是讓 QR 碼可以被掃碼器認出來，但 QR 碼真正厲害的地方在于，即使你這樣、這樣、或者這樣、它都能被正確識別。 現(xiàn)在，我們終于進入到了 QR 碼的核心， Reed-Solomon 編碼。注意，接下來的內(nèi)容會有一點點難，但也只需要中學數(shù)學知識就夠了，如果你理解了會非常有意思，讓我們開始吧。
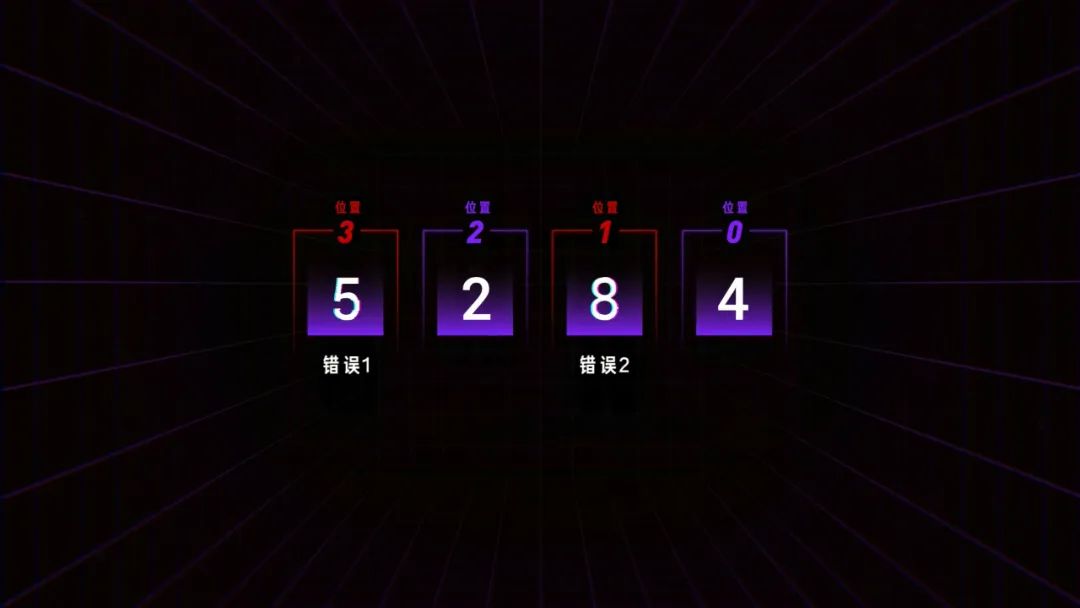
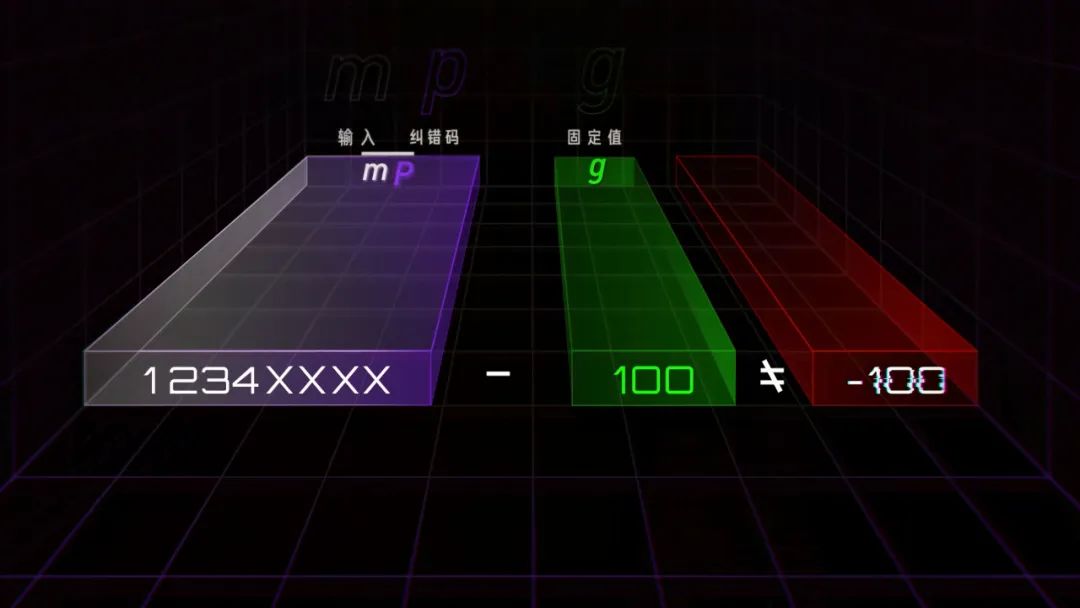
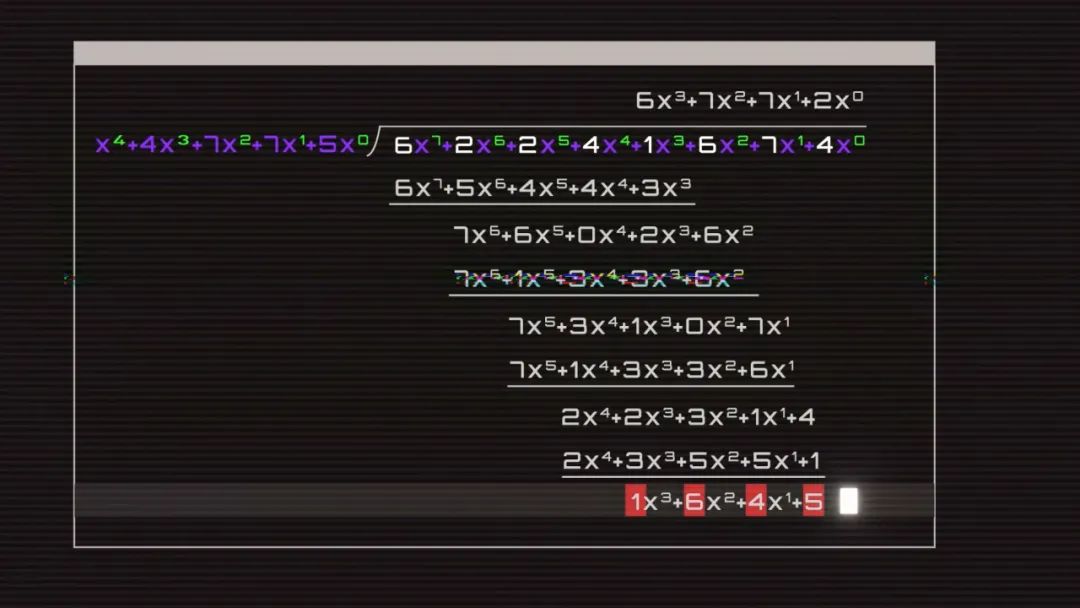
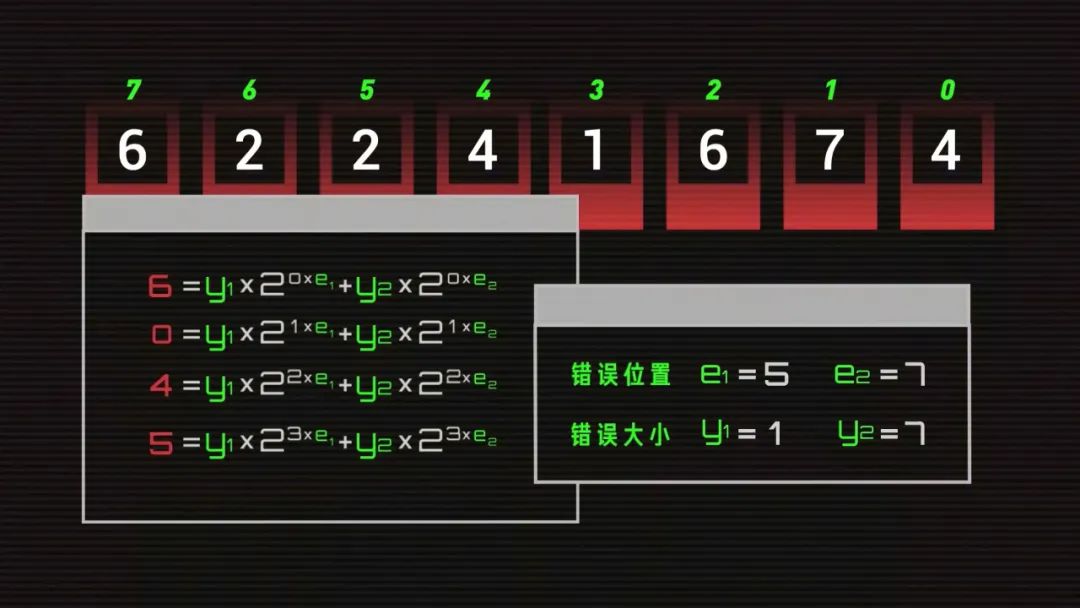
我們知道，二維碼是用黑白方格對應的二進制數(shù)據(jù)來表示信息，比如 1234 就可以編碼為 00011110110100，對應成二維碼里的方格就是這樣。而 Reed-Solomon 編碼可以讓你隨便修改一定數(shù)量的格子，機器都能自動還原成正確的數(shù)據(jù)。為了更好的解釋這一過程，我們簡化成 4 個格子，有 4 個數(shù)字，分別是 1、2、3、4。我們的目標是，任選 2 格修改成其他數(shù)字，算法都可以自動發(fā)現(xiàn)錯的是哪一個，并且還原成修改前的數(shù)據(jù)。為了做到這件事，我們需要得到 4 個變量，錯誤的兩個格子的位置，e1 和 e2，這兩個格子錯誤的大小 y1 和 y2。假設我們知道 e1=3，e2=1，y1=-5，y2=1，那么機器就可以自動調(diào)整成正確數(shù)據(jù)了。而在計算這 4 個未知數(shù)之前，還得先讓機器知道，這串數(shù)字錯了。最簡單的方法，就是算 0。算出了 0 就是對的，不是 0 就是錯的。比如我們所有人的設備都可以保存一個固定數(shù)值 g=1234，用輸入數(shù)值 m 1234 減固定值 g 1234 就剛好等于 0。但 g 是不會變的，如果我們想輸入 5678，結(jié)果就不是 0 了。這時我們就需要根據(jù)輸入值和固定值反推出一個 p，無論我們想輸入什么，都能算出 0，這個 p 就是糾錯碼。比如固定數(shù)值 g= 100，輸入值是 5678，那 p 就可以是 -5578，如果我們輸入變成 1234，p 就會跟著變成 -1134。這樣，如果輸入值被篡改了，比如被改成了 6234，結(jié)果就不是 0，而是 5000，機器就知道輸入錯了。糾錯碼 p 和輸入值 m 都會出現(xiàn)在二維碼上，但這樣就帶了一個新問題，糾錯碼被修改了怎么辦？如果 m+p-100 不等于 0，我們永遠不可能知道是 m 錯了還是 p 錯了，但是如果我們可以把 m 和 p 組合成一個數(shù)字比如說 1234XXXX 呢？聽起來不錯，但這樣減法就不行了，這 4 位數(shù)不管是多少都不可能得到 0，那怎么辦？比如我們讓 12340000 除以 3，余數(shù)等于 1，我們用 12340000 減去 1，就得到了 12339999，此時除以 3 的余數(shù)等于 0。但這樣帶來了兩個新問題， 3 的倍數(shù)有很多，很多錯誤情況下一樣可以得到 0，而即使我們得到了一個余數(shù)，我們又怎么能通過余數(shù)知道哪一位數(shù)錯了多少呢？這時，我們就需要改變計算規(guī)則了。隆重介紹——伽羅瓦域(Galois Field，GF)。伽羅瓦域厲害的地方在于，這是一個封閉的世界，里面的有限個數(shù)字不管怎么算都不會得到它們之外的結(jié)果。以 GF(2^3) 域為例，一共有 8 個數(shù)，「0、1、2、3、4、5、6、7」，他們對應的二進制是這樣。伽羅瓦域的加法和減法運算一樣，都是異或算法。比如 1-2 就是 001 異或 010，結(jié)果是 011，根據(jù)這個表 011 是 3，1+2 結(jié)果也一樣。6+7 就是 1，不管怎么加減，都只能得到這個域里的數(shù)字。而乘除法的規(guī)則復雜一些，結(jié)果大于 7，比如 6*7 就需要對 110 和 111 做模二乘法，再用模二除法除以提前預設的數(shù)值 1011，得到余數(shù) 100，就是 4。這就是伽羅瓦域 GF(2^3) 的完整乘法表，不管你怎么算，永遠只能得到 0、1、2、3、4、5、6、7。除法也類似。還記得剛剛的除法嗎？現(xiàn)在如果我們用伽羅瓦域的規(guī)則，就不能再用 12340000 了，這個世界里只能有這 8 個數(shù)字，那我們還能怎么表現(xiàn) 12340000 呢？在多項式中，我們可以把每個格子里的數(shù)字作為 x 的系數(shù)，把格子的位數(shù)作為 x 的次方數(shù)。比如 1、2、3、4 就是 1*x^3+ 2*x^2+ 3*x^1+ 4*x^0，那么 12340000 的多項式 m(x) 就是這樣既然輸入數(shù)據(jù)變成了多項式，我們要除以的固定值 g 也應該是一個有 x 的多項式。我們要得到的 4 位糾錯碼， g(x) 就有 4 個因子，分別是x減2的零次方，x減2的一次方，x減2的二次方，x減2的三次方，這樣做的意義在于，因為這個 g(x) 展開后的多項式最高位就是 x 的 4 次方，所以我們用 m(x) 除以 g(x) 能剛好就得到 4 位數(shù)的余數(shù)P(x)= 1*x^3 + 6*x^2 + 7*x + 4，把多項式的系數(shù)換成數(shù)字就是 1674。我們兩邊都乘 g(x) ，再把余數(shù) P(x) 移到左邊，別忘了伽羅瓦域里加和減是一樣的。所以我們可以神奇地發(fā)現(xiàn)，把原來的 M(x) 和余數(shù) P(x) 相加，得到的新多項式剛好可以被整除，而這 4 位余數(shù)就是我們要找的 4 位糾錯碼。這樣我們得到了最終的輸入數(shù)據(jù) 12341674，用多項式表示就是這樣好，我們的準備工作已經(jīng)全部完成了。現(xiàn)在，你可以隨便修改這 8 個格子里的 2 個數(shù)，機器都可以完成自動修正。首先，系統(tǒng)會把收到的輸入數(shù)據(jù)變成多項式，除以提前設定好的 g(x) ，得到余數(shù) 1645，不等于 0，說明輸入數(shù)據(jù)有誤。現(xiàn)在，只需要找到錯誤位置 e1、e2 以及他們對應的錯誤大小 y1、y2 就行了。我們知道正確的輸入數(shù)據(jù) M(x) 除以 g(x) 的余數(shù)是 0，那么 M(x) 就等于 g(x) 乘一個固定值 h。如果 g(x)=0， 正確的 M(x) 也會等于 0。而根據(jù) g(x) 的公式，恰好有 4 種情況會等于 0。分別是 x 等于 2 的 0 次方 1 次方 2 次方和 3 次方，用公式寫出來就是這樣：雖然我們不知道正確情況下 m1、m2、m3、m4、p1、p2、p3、p4 是多少，但是我們知道錯誤情況下的，把我們收到的輸入數(shù)據(jù) 62241674 帶入這 4 個方程計算，能得到 4 個不等于 0 的結(jié)果。而這 4 個方程之所以不等于 0，是因為有 2 個地方的數(shù)字出錯了，出錯的大小 y 乘 2 的 n 次方后相加就是方程的結(jié)果。而這 2 的這個 n 次方又和出錯數(shù)字的位置有關，如果 x=2^1 ，那么 n 就等于 1 乘出錯的位置 e，如果 x=2^2 ，那么 n 就等于 2 乘出錯的位置 e。用公式寫出來就是這樣：現(xiàn)在，我們有四個方程組，四個未知數(shù)，機器就能算出來現(xiàn)在，我們可以把收到數(shù)據(jù)的第 5 和第 7 位的數(shù)字 2 和 6，分別和 y1 和 y2 做異或運算，得到 3 和 1，填回去，我們就得到正確的輸入數(shù)據(jù)了。需要說明的是，這是一個簡化后的計算過程，實際情況還要更復雜。這就是二維碼的秘密，把信息編碼為二進制，按順序填上原始數(shù)據(jù)，再填上計算后的糾錯碼，和其他信息，再和掩碼做一次異或運算，最終成為你看到的樣子，一個可靠的碼。 1960 年，工程師 Irving S. Reed 和 Gustave Solomon 可能也不會想到，他們發(fā)布的這篇不到的 5 頁論文會在 60 年后成為當代生活不可或缺的一部分，和無數(shù)精彩絕倫的論文一樣，成為這個世界底層看不見的一塊磚。 
